Handelingsmodel

Voor de studie heb ik het handelingsmodel moeten uitwerken tijdens het thema gecijferdheid.

In onderstaande tekst worden de verschillende niveaus van het handelingsmodel doorlopen om in het laatste niveau, formeel handelen, te komen van de som die hieronder staat afgebeeld. Deze som komt uit de methode ‘de wereld in getallen, versie 4’, groep 3. Het doel dat de methode richting de leerlingen verwoordt, is: Je oefent erbijsommen en erafsommen die op elkaar lijken.

 

Informeel handelen in werkelijkheidssituaties

Binnen het handelingsmodel is het eerste niveau het handelen. De leerlingen voeren de opdracht uit door te doen. In groep 3 hebben de leerlingen de hoeveelheid 10 leren kennen door het gebruiken van een volle eierdoos. Bij de som 1+5 hebben de leerlingen een eierdoos met daarin één ei. De leerling vult deze doos aan met vijf eieren en ziet dat er dan zes eieren in de doos zitten. Het uitvoeren van deze opdracht gebeurt met eierdozen en houten eieren. De oplossing van de som blijft staan en er worden nieuwe eierdozen en eieren gepakt. De leerling start met een volle eierdoos met tien eieren en een eierdoos met daarin één ei. Daarna pakt de leerling vijf eieren en vult de eierdoos met maar één ei verder aan. Er is te zien dat er nu 16 eieren in totaal zijn. Door de eerdere oplossing te laten staan, ziet de leerling de overeenkomst tussen de eierdozen.

Voorstellen – concreet

In het tweede niveau van het handelingsmodel komt de situatie van het eerste niveau terug op papier. De leerlingen kunnen de situatie zelf op papier tekenen of zichzelf vanaf papier een voorstelling maken van de situatie (Van Groenestijn, Borghouts & Jansen, 2011). Voor het voorstellen kan ook gebruik gemaakt van het digibord. Via het digibord kunnen de leerlingen de situatie namaken. Dit kan bijvoorbeeld met de digibordsoftware van Gynzy.

 

Voorstellen – abstract

Het derde is niveau binnen het handelingsmodel is het abstract voorstellen van de situatie. Op dit niveau kunnen de leerlingen de situatie abstract weergeven (Van Groenestijn, Borghouts & Jansen, 2011). De leerlingen kunnen een tekening maken van de som die zijn zien en kunnen benoemen wat er gebeurd. Er wordt door de leerlingen gezegd of het een plus- of minsom is en wat dit betekent voor de hoeveel: wordt het meer of minder? Van Groenestijn, Borghouts & Jansen (2011) geven aan dat het essentieel is dat leerlingen kunnen toelichten waarom ze iets doen en of ze weten wat de tekening in het rekenboek betekend.
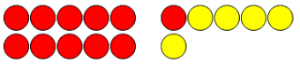
Het kan ook zo zijn dat de leerlingen op dit niveau gebruik maken van fiches om de situatie abstract weer te geven (Van Groenestijn, Borghouts & Jansen, 2011). De leerlingen leggen de fiches dan neer in de structuur van de eierdoos om de situatie na te bootsen. In groep 3 worden fiches gebruikt met twee kleuren, deze geven de leerlingen de mogelijkheid duidelijker te maken welke fiches gebruikt zijn als aanvulling.

Formeel handelen

Het formeel handelen is dat de leerling de kale sommen kan oplossen. De leerlingen kunnen de sommen oplossen, maar kunnen hierbij nog gebruik maken van denkmodellen (Van Groenestijn, Borghouts & Jansen, 2011).

 

Literatuur
Groenestijn, van M., Borghouts, C. & Janssen, C. (2011). Protocol Ernstige RekenWiskundeproblemen en Dyscalculie: BAO SBO SO. Assen: Koninklijke van Gorcum.

 

Dit bericht bevat affiliate links.